Primitives of a Network

Begriffe zur Graphentheorie und zu Netzwerken

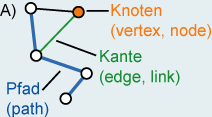
Mit Graphen ist eine umfangreiche Begrifflichkeit verknüpft, die meisten Begriffe haben aber eine einfache Definition. Ein Graph besteht aus einer Menge von Knoten V und Kanten E (Beispiel: Graph A). Knoten repräsentieren Objekte, die Namen und andere Eigenschaften haben können, z. B. eine Umsteigestation in einer U-Bahn. Eine Kante ist eine Verbindung zwischen zwei Knoten z. B. die Flugverbindung zwischen Zürich und Berlin. Zwei Knoten sind benachbart (engl. adjacent), wenn sie durch eine Kante verbunden sind. 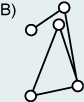Graphen können visualisiert werden, indem man die Knoten durch Punkte und diese durch Linien verbindet, welche die Kanten darstellen (Graphen A–K). Dabei darf man nicht vergessen, dass der Graph unabhängig von der Darstellung definiert ist. Die beiden Figuren A und B stellen den gleichen Graphen dar.
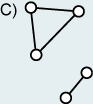
Ein Pfad von Knoten s zu Knoten e in einem Graph ist eine Liste von benachbarten Knoten. Ein einfacher Pfad ist ein Pfad, auf dem sich keine Knoten wiederholen. Ein zusammenhängender Graph besitzt von jedem Knoten zu einem anderen Knoten einen Pfad. Ein nicht zusammenhängender Graph zerfällt in zusammenhängende Komponenten (Graph C).

Elemente eines Graphen	zusammenhängend	nicht zusammenhängend

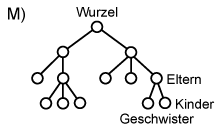
Ein Zyklus ist ein einfacher Pfad, bei dem der erste und der letzte Knoten identisch sind (Graph E). Ein Graph ohne Zyklen wird Baum genannt (Graph K). Bäume haben eine hierarchische Struktur und werden oft explizit so dargestellt.
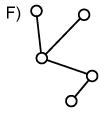
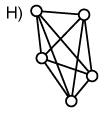
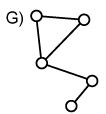
Graphen, in denen alle Kanten vorhanden sind, werden vollständige Graphen genannt (Graph F). Graphen mit relativ wenigen Kanten bezeichnet man als licht; Graphen, bei denen relativ wenige der möglichen Kanten fehlen, werden als dicht bezeichnet. Gewichtete Graphen (Graph G) sind Graphen, bei denen den Kanten Zahlenwerte (Gewichte) zugewiesen werden, um Entfernungen (zeitlich oder geometrisch) oder Kosten darzustellen. Dadurch werden mit dem Graphen mehr Informationen verknüpft.

Ungerichtete Graphen:

	zyklisch	vollständig	gewichtet

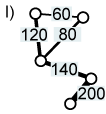
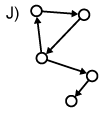
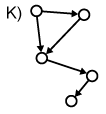
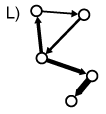
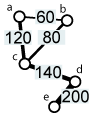
In gerichteten Graphen sind Kanten "Einbahnstrassen" (Graph H); eine Kante kann von x nach y führen, aber nicht von y nach x. Gerichtete Graphen ohne gerichtete Zyklen (gerichtete Zyklen: alle Kanten zeigen in die gleiche Richtung) werden gerichtete azyklische Graphen genannt (Graph I). Gerichtete gewichtete Graphen werden Netzwerk genannt (Graph J). Umgangssprachlich und in der Geographie wird der Begriff des Netzes oder Netzwerks (engl. network) jedoch oft für alle Arten von Graphen verwendet.

Gerichtete Graphen:

zyklisch	azyklisch	gerichtet + gewichtet = Netzwerk	hierarchisch

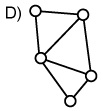
Es werden zudem planare von nicht-planaren Graphen unterschieden werden. Bei planaren Graphen handelt es sich um solche, die auf einer Ebene abgebildet werden können, ohne dass ihre Kanten sich schneiden (vgl. Abbildung E. im Gegensatz zu Abbildung F.).

Planare vs. nicht-planere Graphen:

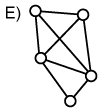planar	nicht-planar

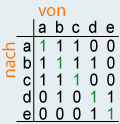
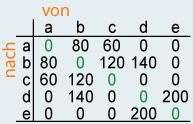
Eine weitere einfache Darstellungsform für Graphen, die auch von einem Digitalrechner bearbeitet werden kann, ist die Adjazenzmatrix (engl. adjacency matrix). Es wird eine Matrix von der Grösse VxV definiert, wobei V die Anzahl der Knoten ist. Die Felder werden auf 1 gesetzt, wenn eine Kante zwischen den Knoten z. B. a und b existiert, und auf 0, wenn keine solche Kante vorhanden ist. Im Beispiel gehen wir davon aus, dass von jedem Knoten eine Kante zu sich selbst existiert. Ob man die Diagonale auf 1 oder auf 0 setzt, ist vom Verwendungszweck abhängig. In manchen Fällen ist es günstiger, die Diagonalen auf 0 zu setzen. Die Matrix heisst Adjazenzmatrix, weil die Struktur dieser Matrix angibt, welche Knoten benachbart sind (d. h. adjazent). Etwas Ähnliches ist mit Gewichten möglich: Dann werden anstelle des Werts 1 die Gewichte in die Felder geschrieben.

Adjazenzmatrix	Matrix mit Gewichten

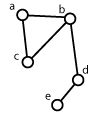
Im Zusammenhang mit der Beschreibung und Analyse von Netzen wird oft der Begriff der Topologie (engl. topology) gebraucht. Dieser Begriff und die zugehörigen Konzepte werden im Modul "Räumliche Modellierung" ausführlich erläutert. Die in untenstehender Abbildung dargestellten Netze besitzen topologisch äquivalente Verbindungen, d.h. es handelt sich um 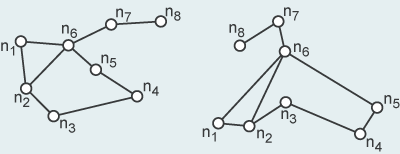topologisch äquivalente Graphen.

Zwei topologisch äquivalente Graphen