Distance-based interpolation

In the simplest case, we can proceed with distance-based methods the same way as with the "moving windows" method: we define a certain "neighborhood" of known data points around the unknown position to be estimated each time; the arithmetic mean of these known measurement values is our estimate (= moving average). The neighborhood can be defined in different ways:

• A spatially fixed shape (rectangle, circle, etc.)
• A certain number of nearest neighboring points

However, this method is quite fuzzy because of the different distances between the position to be estimated and the poor integration of known points in the interpolation. The actual distance-based methods use exactly these distances between the estimation points and the known measurement points to weigh their influence in the calculation of the estimated value. By the way, they require a linear spatial correlation between the phenomena.

Using the so-called "Inverse Distance Weighting" method or IDW, the weight of any known point is set inversely proportional to its distance from the estimated point. It is calculated as follows:

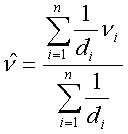Inverse Distance Weighting IDW – basic formula

$\hat{v}$ = value to be estimated $v_i$ = known value di..., dn= distances from the n data points to the point estimated n

In most cases, you will find the following variation, in which the influence of the distance can be additionally controlled by an exponent (which is preset to 2 in most programs).

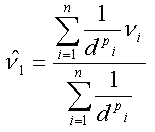Most common form of IDW formula with added distance weighting exponent

$\hat{v}$= value to be estimated $v_i$= known value dpi..., dpn = distances from the n data points to the power of p of the point estimated

The lower the exponent, the more uniformly all neighbors are incorporated into the calculation (regardless of their distance), and therefore, the "smoother" the estimated surface. The higher the exponent, the more accentuated and "unsettled" is the surface because only the weight of the nearest neighbors is integrated in the interpolation (see the following interactive animation).

Advantages of the IDW interpolation:

• It allows for very fast calculations
• Different distances are integrated in the estimation
• The distance-weighting exponent is able to precisely control the influence of the distances

Disadvantages of the IDW interpolation:

• It is not possible to do a direction-dependent weighting. That means that spatially oriented relationships are ignored (e.g. elevation points along a ridge).
• Unsightly artefacts are the so-called "Bulls-eyes" – these are circular areas of equal values around the known data points. However, applying a variation of the IDW-Interpolation developed by Shepard (1968) can reduce the Bulls-eyes:

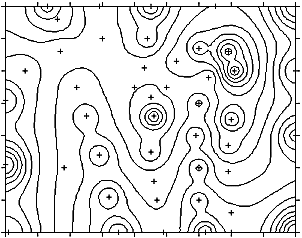IDW "Bulls eye" effect: concentric areas of the same value around the known points – an unwanted artefact of the IDW interpolation.

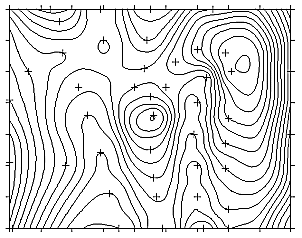IDW modified after Shepard: the Bulls-eyes are definitely reduced.