Classification of Data

Classified versus unclassified data

PLEASE NOTE: this learning object "Classification of Data" is currently under revision. Several sections are therefore missing at the moment (marked with [...] ). The remaining text is mainly based on (Slocum 1999).

As you have seen in the previous paragraph about "data levels", numerical data consists of the exact indication of measured information. As you may imagine, such measurable information is very important for geographical data analysis and for precise value presentations on maps. However, for an optimal analysis of numeric data we sometimes need to classify our dataset with a method for an appropriated thematic map presentation, which allows an optimal map analysis of numeric data. In this section, we will reveal when we need to classify data, and when we can work with unclassified data.

What is a classified map?

A classified map represents data that has been grouped into different classes. On the map, the different classes can be distinguished e.g. by different colours (hue, brightness, or saturation).

Why can it be useful to classify data before creating a map?

The human eye only has a limited ability to discriminate a large number of different areal symbol shades. Due to this fact, it is sometimes essential to classify quantitative thematic map content. This allows us to create a smaller number of data classes and to choose symbol shades that can be distinguished easily.

What is the difference between a classified and an unclassified map?

Classified maps consist of colour shades that are generally based on the conventional "maximum-contrast" approach, using equally spaced tones from one class to another. Thanks to this method, the classified map does not reveal a huge and inhomogeneous range of colour variations.

[...]

Thus, we finally have to decide when we choose to classify our collected data and when not. You should have considered two criteria when you decide whether you create a classified or an unclassified map presentation:

1. Do you wish to maintain numerical data relations? If you wish to create a map that maintains the data relation, unclassified data theoretically does a better job than classified data, as unclassified data allows us to maintain the numerical relations between data. This means that the colour shades on an unclassified map are directly proportional to the values of each enumeration unit.
2. Is your map intended to be used for data presentation, or is it meant to be applied for data analysis? When you create a map that will be used for a simple data presentation, you basically have the choice between either classified or unclassified data. When you decide to use classified data for your map, however, the differences in value and colour shade usually become more obvious. In general, cartographers do not approve the result of non-classified data, since unstructured (or non-generalised) maps are composed of many individual symbols. Quite contrary to this, it is advisable not to use more than six classes, so that the map reader is able to distinguish them easily.

However, if the map you create is intended for data analysis, it is worth comparing a large variety of visual classification approaches. You do this in order to choose the best method for your specific thematic analysis. This map comparison may possibly include unclassified maps, too.

Major Classification Methods

For thematic map presentation, the acquired and analysed thematic data values are often grouped into classes, which simplify the reading of the map as we have learned in the previous section. If you decide to classify your data, you may wonder, what would be the best method. For this purpose, we will repeat and refresh the basics of your knowledge about statistical methods in the following. The major methods of data classification are:

• Equal intervals,
• Mean-standard deviation,
• Quantiles,
• Maximum breaks and
• Natural breaks

[...]

The Equal Interval Classification (constant class intervals)

In this classification method, each class consists of an equal data interval along the dispersion graph shown in the figure. To determine the class interval, you divide the whole range of all your data (highest data value minus lowest data value) by the number of classes you have decided to generate.

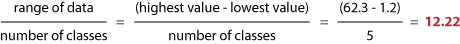
After you have done that, you add the resulting class interval to the lowest value of your data-set, which gives you the first class interval. Add this interval as many times as necessary in order to reveal the number of your predefined classes.

When is it useful to choose the method of equal class intervals?

It is appropriate to use equal class intervals when the data distribution has a rectangular shape in the histogram. This, however, occurs very rarely in the context of geographic phenomena. Moreover, it is useful to use this method when your classification steps are nearly equal in size. The major disadvantage of this method is that class limits fail to reveal the distribution of the data along the number line. There may be classes that remain blank, which of course is not particularly meaningful on a map.

The Mean-Standard Deviation Classification

Another method that allows us to classify our dataset is the standard deviation. This method takes into account how data is distributed along the dispersion graph. To apply this method, we repeatedly add (or subtract) the calculated standard deviation from the statistical mean of our dataset. The resulting classes reveal the frequency of elements in each class.

The mean-standard deviation method is particularly useful when our purpose is to show the deviation from the mean of our data array. This classification method, however, should only be used for data-sets that show an approximately "standardised normal distribution" ("Gaussian distribution"). This constraint is the major disadvantage of this method.

The Quantiles Classification

Another possibility to classify our dataset is to use the method of quantiles. To apply this method we have to predefine how many classes we wish to use. Then we rank and order our data classes by placing an equal number of observations into each class. The number of observations in each class is computed by the formula:

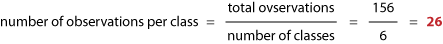
If no integer values are resulting from this division, we attempt to place approximately the same number of observations in each class.

An advantage of quantiles is that classes are easy to compute, and that each class is approximately equally represented on the final map. Moreover, quantiles are very useful for ordinal data, since the class assignment of quantiles is based on ranked data. The main disadvantage of this classification method are the gaps that may occur between the observations. These gaps sometimes lead to an over-weighting of some single detached observations at the edge of the number line.

The Maximum Breaks Classification

When we choose to use the method of maximum breaks we first order our raw data from low to high. Then we calculate the differences between each neighboring value, when the largest value differences will be applied as class breaks. You can also recognise the maximum breaks visually on the dispersion graph: large value differences are represented by blank spaces.

One advantage of working with this method is its clear consideration of data distribution along the number line. Another advantage is that maximum breaks can be calculated easily by subtracting the next lower neighboring value from each value. A disadvantage, however, is that the systematic classification of data misses any proper attention to a visually more logical and more convenient clustering (see "Natural breaks").

The Natural Breaks Classification

Applying the classification method of "natural breaks”, we consider visually logical and subjective aspects to grouping our data set. One important purpose of natural breaks is to minimise value differences between data within the same class. Another purpose is to emphasize the differences between the created classes.

A disadvantage of this method is that class limits may vary from one map-maker to another due to the author's subjective class definition (Slocum 1999). The Jenks-Caspall Alorithm formalizes this procedure and is often used in GIS software.

Discussion of the Classification Methods

Equal intervals

Particularly useful when the dispersion graph has a rectangular shape (rare in geographic phenomena) and when enumeration units are nearly equal in size. In such cases, orderly maps are produced.

Mean-standard Deviation

Should be used only when the dispersion graph approximates a normal distribution. The classes formed, yield information about frequencies in each class. Particularly useful when the purpose is to show deviation from the array mean. Understood by many readers.

Quantiles

Good method of assuring an equal number of observations in each class. Can be misleading if the enumeration units vary greatly in size.

Maximum Breaks

Simplistic method which consider how data are distributed along the dispersion graph and group those that are similar to one another (or, avoid grouping values that are dissimilar). Relatively easy to compute, simply involving subtracting adjacent values.

Natural Breaks

Good graphic way of determining natural group of similar values by searching for significant depressions in frequency distribution. Minor troughs can be misleading and may yield poorly defined class boundaries.