|
|
Spatial Dynamics - Discontinuous case
![]() Cellular automata were invented in the late 1940s by two mathematicians,
John von Neumann and Stanislaw Ulam, working at the Los Alamos National
Laboratory in the United States. Cellular Automata (CA) are dynamic systems
which are discrete in space and time, operate on a uniform, regular lattice and
are characterised by "local" interactions.
Cellular automata were invented in the late 1940s by two mathematicians,
John von Neumann and Stanislaw Ulam, working at the Los Alamos National
Laboratory in the United States. Cellular Automata (CA) are dynamic systems
which are discrete in space and time, operate on a uniform, regular lattice and
are characterised by "local" interactions.
A CA system consists of a regular grid of cells; each can be in one of a finite number updated synchronously in discrete time steps:
- The state of a cell is determined by the previous states of the surrounding neighbourhood of cells.
- Each cell in a regular spatial lattice can have any one of a finite number of states.
- Local rule: the state of a cell at a given time depends only on its own state one time step previously and states of its nearby neighbours at the previous time step. The state of the entire lattice advances in discrete time steps
Different kind of problems can be approached using cellular structure and
rules: spatially complex systems (e.g., landscape processes),
discrete entity modelling in space and time (e.g., ecological systems,
population dynamics) or emergent phenomena (e.g., evolution, earthquakes)
CA consist of different elements, they are:
- Cell Space: it is one cell that can be in any geometric shape.
- Cell State: can represent any spatial variable. For greater flexibility into CA, two groups of cell states integrated, fixed and functional.
- Time Steps: CA evolve at a sequence of discrete time steps
- Transition Rules: a transition rule specifies the state of cell before and after updating based on its neighbours conditions. In the classic CA, transition rules are deterministic and unchanged during evolution. Now the rules are modified into stochastic expressions and fuzzy logic controlled methods.
- Spatial neighbourhood: a
 limited neighbourhood (Von Neumann) including 4 adjacent cells or
an
limited neighbourhood (Von Neumann) including 4 adjacent cells or
an  extended neighbourhood (Moore) including the 8 adjacent
cells
extended neighbourhood (Moore) including the 8 adjacent
cells
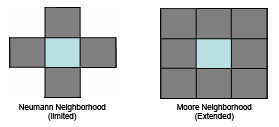 The two considered spatial neighbourhoods: limited neighbourhood (Von Neumann) and extended (Moore).
The two considered spatial neighbourhoods: limited neighbourhood (Von Neumann) and extended (Moore).
As summarised by A.K. Singh (2003), a cellular automata model can be
represented as the following quadruple:

Then the state of a cell at time (t+1) is a function of it state at time t of its neighbourhood and of the set of transition rules:

