1.3.2. Distanz-basierte Interpolation

Im einfachsten Fall dieser Methoden können wir wie bei der „Moving Windows“-Methode vorgehen: Wir definieren eine gewisse „Nachbarschaft“ bekannter Datenpunkte um die jeweils zu schätzende unbekannte Position; das arithmetische Mittel aus diesen bekannten Messwerten ist dann unser Schätzwert (= lokale Mittelwertbildung, moving average). Die Nachbarschaft kann unterschiedlich definiert werden:

• eine räumlich festgelegte Form (Rechteck, Kreis usw.)
• eine bestimmte Anzahl nächst benachbarter bekannter Punkte

Dieses Instrument ist aber recht unscharf, weil die verschiedenen Distanzen zwischen Schätzposition und bekannten Punkten nur unzureichend in die Interpolation einfliessen. Die eigentlichen Distanz-basierten Methoden verwenden eben alle jene Entfernungen zwischen der zu schätzenden Position und den bekannten Messpunkten, um deren Einfluss in der Berechnung des Schätzwertes zu gewichten. Sie setzen übrigens einen linearen räumlichen Zusammenhang zwischen den Phänomenen voraus.

Bei der sogenannten „inversen Distanz-Gewichtung “(Inverse Distance Weighting, IDW) wird das Gewicht jedes bekannten Punktes invers proportional zu seiner Entfernung zum geschätzten Punkt gesetzt. Die Berechnung erfolgt nach dieser Formel:

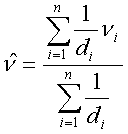Inverse Distanz-Gewichtung (IDW) – Grundformel

ν ... zu schätzender Wert, νi ... bekannte Werte di..., dn... Distanzen der n Datenpunkte zum geschätzten Punkt

Meist finden Sie die folgende Variante, in welcher der Einfluss der Distanz zusätzlich über einen Exponenten gesteuert werden kann (dieser wird in den meisten Programmen auf 2 voreingestellt):

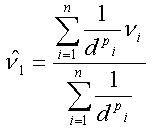Häufigste Form der IDW-Formel mit zusätzlichem Distanzgewichtungs-Exponenten

ν ... zu schätzender Wert, νi ... bekannte Werte dpi..., dpn... mit p exponenzierte Distanzen der n Datenpunkte zum geschätzten Punkt

Je niedriger der Exponent gesetzt wird, desto gleichförmiger gehen alle Nachbarn (ungeachtet ihrer Distanz) in die Berechnung ein, und desto „glatter“ wird die Schätzoberfläche. Je höher der Exponent wird, desto akzentuierter und „unruhiger“ wird die Oberfläche, da nur mehr das Gewicht der nächstgelegenen Nachbarn in die Interpolation einfliesst (siehe folgende interaktive Animation).

IDW-Schätzoberflächen der Schweizerischen Niederschlagsdaten

Vorteile der IDW-Interpolation:

• Sie ermöglicht sehr schnelle Berechnungen.
• Unterschiedliche Distanzen fliessen in die Schätzung unterschiedlich ein.
• Über den Distanzgewichtungs-Exponent kann der Einfluss der Distanzen fein gesteuert werden.

Nachteile der IDW-Interpolation:

• Es ist keine richtungsabhängige Gewichtung möglich, d. h. räumlich gerichtete Zusammenhänge werden ignoriert (z. B. Höhenpunkte entlang eines Bergrückens).
• Unschöne Artefakte sind die sogenannten „Bull-Eyes“ – dies sind kreisförmige Bereiche gleicher Werte um die bekannten Datenpunkte. Eine von Shepard (1968) entwickelte Variante der IDW-Interpolation reduziert diese Bull-Eyes jedoch (siehe folgende Abbildungen).

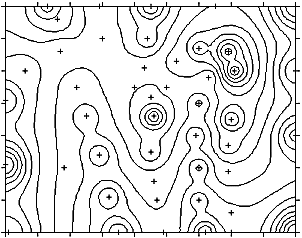IDW „Bull Eyes“-Effekt: Um die bekannten Punkte sind konzentrische Bereiche gleicher Werte zu erkennen – ein unerwünschtes Artefakt der IDW-Interpolation

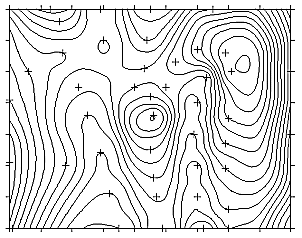IDW modifiziert nach SHEPARD: die Bull-Eyes sind deutlich reduziert