1.3.3. Geostatistische Interpolation
Einer der Nachteile der IDW-Interpolation ist das Fehlen richtungsspezifischer (anisotroper) Informationen. Räumliche Korrelationen werden also ignoriert und fliessen nicht in das Schätzergebnis mit ein. Diesen Nachteil gleichen die geostatistischen Interpolationen aus.
Schon der Name „Geo“-Statistik weist auf das wichtigste Merkmal dieser Methoden hin: räumlich-statistische Parameter bilden die Hauptbasis für diese Interpolations-Verfahren.
Das Variogramm bzw. die Variographie, also die Methode, es aus den räumlichen Punktdaten abzuleiten, bildet die Grundlage für eine erfolgreiche geostatistische Interpolation.
Geostatistische Interpolationen sind fortgeschrittene und teilweise komplizierte Methoden, deren sinnvolle Anwendung eine Menge an Vorwissen und Erfahrung benötigt. Darum müssen an dieser Stelle ein paar Stichworte genügen.
Die wichtigsten Verfahren sind die Kriging-Methoden. Benannt sind sie nach einem südafrikanischen Ingenieur, D. G. Krige. 1951 legte in seiner Diplomarbeit die Grundlagen für Kriging. Aber die Hauptentwicklungen gehen auf die Arbeit von G. Matheron in den 1960er Jahren zurück.
Mittels der Variographie erhalten wir Hinweise darauf, wie ähnlich bzw. unähnlich die Messwerte benachbarter Datenpunkte in Abhängigkeit von ihrer Entfernung zueinander sind.
Variographie
a) Zunächst bilden wir zwischen allen Datenpunkten Paare und vergleichen jeweils deren 2 Werte. Wir wissen pro Datenpaar den Differenzwert (Semivarianz) und die Distanz (h):
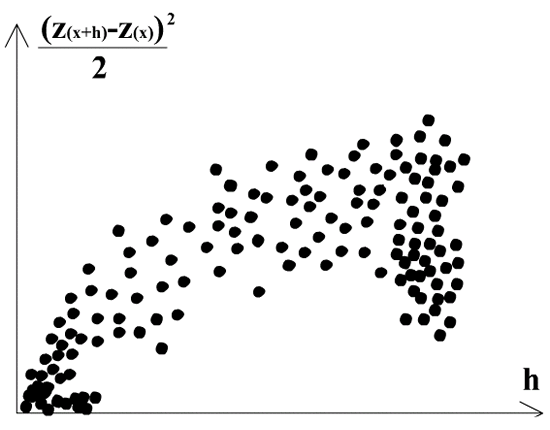Variogramm Wolke, Unterschiede zwischen Datenpunkten versus räumlicher Distanz zwischen diesen Punkten.b) Anschliessend unterteilen wir die Distanzen (x-Achse) in Intervalle (sogenannte Lags) und mitteln die Semivarianzen der darin enthaltenen Datenpaare (rote Punkte). Verbinden wir diese roten Punkte pro Lag, erhalten wir das experimentelle Variogramm. Diese Kurve beschreibt, wie ähnlich sich die Werte zweier benachbarter Positionen in Abhängigkeit von ihrer Distanz zueinander sind:
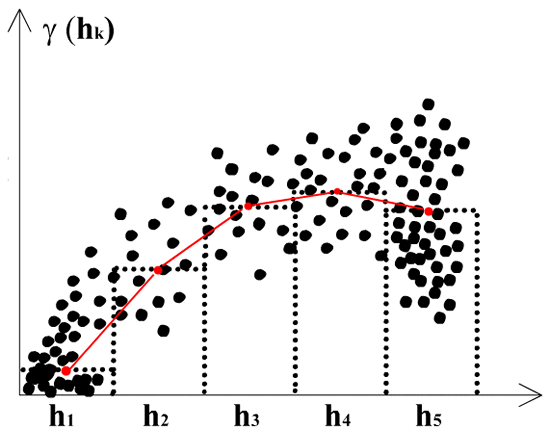Experimentelles Variogramm, die Unterschiede werden pro definierter Klasse (h1 ... h5, = Lagintervalle)
gemitteltc) Um diese Darstellung der räumlichen (Un-)Ähnlichkeit mathematisch besser verarbeiten zu können, legen wir einfache Kurvenfunktionen so an das experimentelle Variogramm an, dass es dieses möglichst gut nachbildet. Diese Kurve nennen wir theoretisches Variogramm:
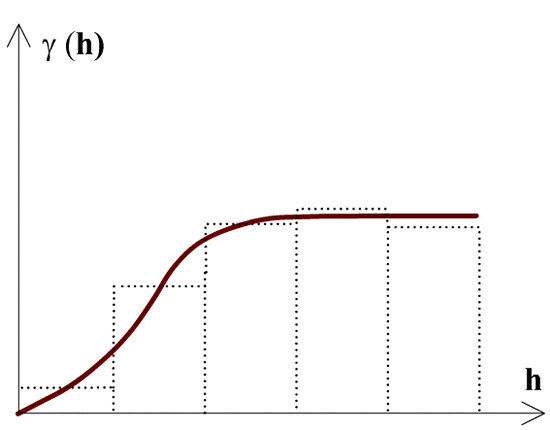Theoretisches Variogramm, eine theoretische Variogrammfunktion wird an die Sequenz der gemittelten Unterschiede
pro Klasse (= pro Lag) angepasstWir behelfen uns nun beim Kriging, indem wir unsere Daten in dieses Modell räumlicher Kontinuität einbauen – jenem Modell, das wir im Zuge der Variogramm-Modellierung entwickelt bzw. gefunden haben. Ausgehend von solch einem Modell können wir für unsere Schätzungen Fehlervarianzen berechnen und deren Minimierung anstreben.
Die Interpolation mit Kriging ist eine Art Kurvenanpassung: Wir haben aus unseren bekannten Datenpunkten ein Modell abgeleitet, wie die räumlichen Zusammenhänge beschaffen sein könnten. Basierend auf diesem Modell schätzen wir nun die unbekannten Punkte. Betrachten wir dies der Einfachheit halber in nur zwei Dimensionen, dann arbeiten wir mit einer Regressionstechnik, einer Kurvenanpassung:
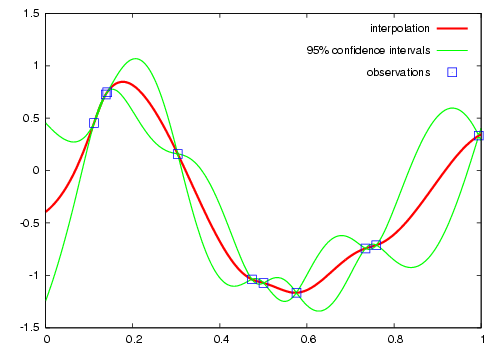Kriging in zwei Dimensionen: Die blau umrandeten Quadrate sind unsere bekannten Datenpunkte, die rote
Linie ist der geschätzte Verlauf, und die grünen Linien repräsentieren die statistischen
Rahmenparameter aus unserem Modell (Wikipedia)Oft hört man den Begriff „exakter Interpolator“ im Zusammenhang mit Kriging, sowie IDW und einigen anderen Schätzverfahren. Damit meint man, dass eine mittels dieser Methoden geschätzte Oberfläche die bekannten Datenpunkte exakt schneidet. Führen wir also die Kriging-Berechnung an einer Position mit bekanntem Wert durch, dann liefert das Kriging-System uns in der Regel genau jenen Wert zurück.
Zum Vergleich sehen Sie nachfolgend das Resultat einer inversen Distanz-Gewichtung dem einer Kriging-Interpolation gegenübergestellt:
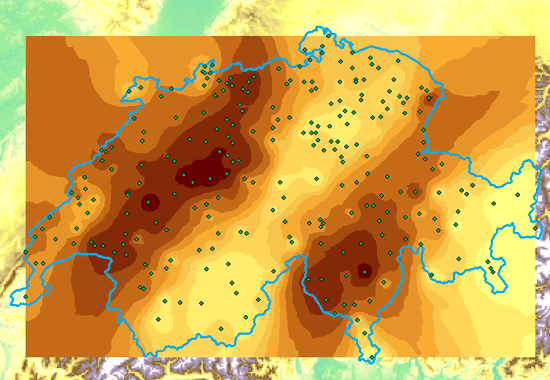Schätzoberfläche aus inverser Distanz-Gewichtung, Datengrundlage sind Schweizer Niederschlagsmesswerte.
Beachten Sie einige „Höfe“, also Bereiche gleicher Werte um bekannte Datenpunkte
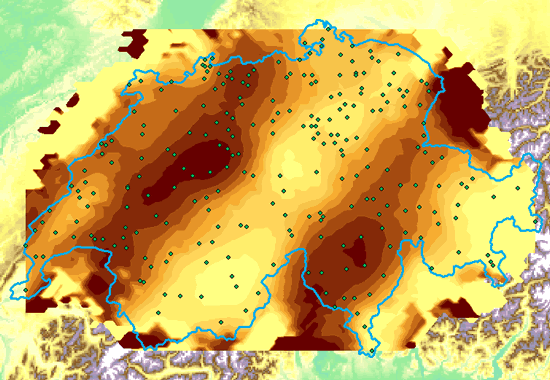Resultat einer Kriging-Interpolation mit Schweizer Niederschlagsmesswerten, hier sind keine Höfe zu
beobachten, denn das Kriging-System „kennt“ räumliche Zusammenhänge. Diese Informationen bezieht es aus
dem VariogrammWeitere wichtige Parameter für Interpolationen: Such-Nachbarschaft
Alle Interpolations-Methoden lassen sich zusätzlich über die Definition einer Such-Nachbarschaft steuern, d. h. wie viele bzw. welche bekannte Datenpunkte werden zur Berechnung einer unbekannten Position herangezogen. Wenn wir diese Nachbarschaft ignorieren, dann beziehen wir sämtliche vorhandenen bekannten Daten in die Schätzung jedes Punktes mit ein. Im Fall der Schweizerischen Niederschlagsdaten hiesse dies, dass zur Berechnung eines Niederschlagswertes im Tessin auch die Werte der Messstationen aus dem Jura einfliessen. Dass dies wenig Sinn ergibt, liegt nahe.
  |
 |
 |