|
|
|
|
|
|
Choroplethic maps
Definition
Chorophletic maps are used to show relations, also called ratio numbers, between two values. In most of the cases the denominator is an area. However, ratio numbers can also be calculated from two non area-related values, but the absolute numbers somehow have to be in relation with their reference area, as it is styled depending on the value of the ratio number. An example of the first-mentioned variant is the population per square kilometre (population density) on community level. An example for the second variant is the ratio between protestants and catholics on district level Choroplethic maps (Witt 1967, p. 186).
 Choroplethic map according variant 1 (Institut für Kartografie 2004) Choroplethic map according variant 1 (Institut für Kartografie 2004) |
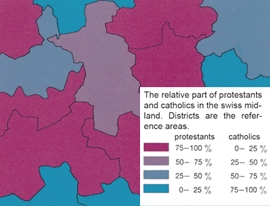 Choroplethic map according variant 2 (Imhof 1972) Choroplethic map according variant 2 (Imhof 1972) |
Choroplethic maps are unsuitable for the symbolisation of
graded absolute values. They distort the message of the map because the map
viewer automatically takes into account the size of the areas. In this case
large areas with a low absolute value get too much importance whereas the
importance of small areas with a high absolute value is too small. For the
depiction of absolute values diagram maps should be used (see the following
section). A similar case occurs when the denominator of ratio numbers is not
the corresponding area. The figure above shows, which confession dominates in
a specific area. The map tempts the viewer to interpret a high absolute value
for large areas with a high density.
Characteristics of choroplethic maps
Representation
The areas, to which the ratios are related, are styled with different fill
colours or patterns. The more dense an object is distributed within an area the darker
the colour or the more dense the pattern should be.
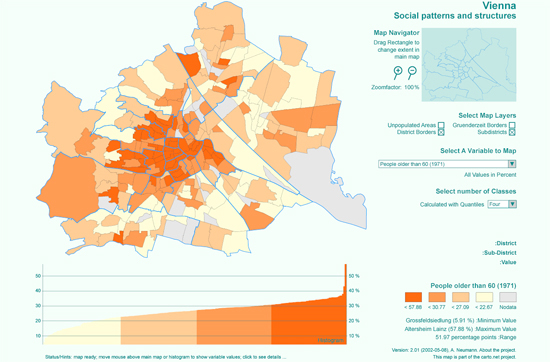
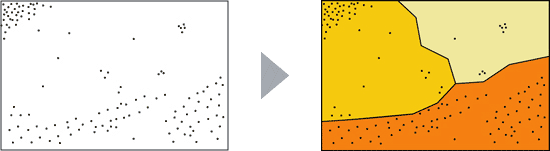
The following figure shows an example of a choroplethic map. With a click on the map you get to the corresponding interactive map. On its basis you can get familiar with the characteristics of choroplethic maps.
Value classes
The ratios or densities are normally classified in value classes. Areas get the same styling if their values are in the same class. The optimal number of classes varies for each dataset. To maintain a good readability of the map, the colours of the classes have to be clearly distinguishable.
Types of choroplethic maps
Choroplethic maps are classified by their reference areas:
- Choroplethic maps based on administrative areas.
- Dasymetric maps show densities of areas regarding geographic properties.
- Choroplethic maps in relation to geometric areal units such as grid squares.
Below all three map types are described in details.
Choropleth maps
Properties
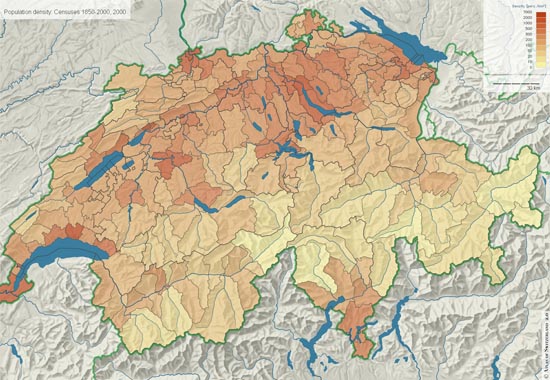
The shown densities in these maps are relative to given administrative areas such as communities, districts, cantons or even countries and continents. The following figure is an example of this map type and depicts the population density of Switzerland on district level.
The selection of the administrative reference area, the value classes and class limits play an important role during the mapping process. With a specific selection of these parameters the appearance and significance of a map can be highly influenced. Density differences can be emphasized or suppressed.
Advantages and disadvantages of choropleth maps
Advantages
- Statistical data can be visualised quickly as they are generally related to administrative areas.
- The choropleth method is applicable to any scale, as long as the individual areas are not getting too small. If this is the case, there is the possibility to switch to a higher administrative level (Imhof 1972, p. 166).
Disadvantages
- Choropleth maps assume a constant density within the depicted area. If the real object density varies, the expressiveness of the map gets distorted. For the example of the population density this is the case in mountain regions, where the populated area is usually only a fraction of the administrative area. The following example demonstrates this problem: the most dense area is not visible, because it gets cancelled out by less dense areas within the same administrative area.
- Comparisons of different datasets from different years are possibly difficult
because administrative areas may vary over time (communities can be consolidated
or split up etc.).
Dasymetric maps
Characteristics
Dasymetric maps are also called "choropleth maps according to the geographic method" (Imhof 1972, p. 167).
In contrast to choropleth maps this map type does not use administrative
but geographical areas which are formed by considering the real distribution of
the objects.
The following part of a map depicts a dasymetric visualisation.
Click on the figure to view the whole map.
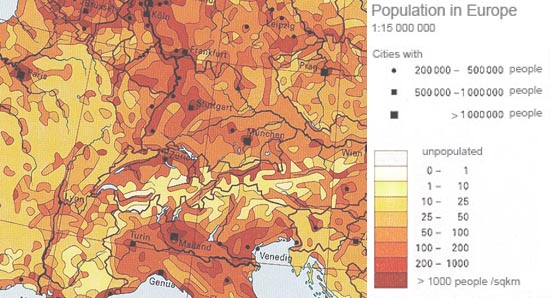 Soruce: (Spiess 2004)
Soruce: (Spiess 2004)Construction methods
There exist several methods to construct dasymetric maps. Most of them use dot maps as a basis. Detailed explanations of the different construction methods can be found here (only available in German).
Advantages and disadvantages of dasymetric maps
Advantages
- In contrast to choropleth maps dasymetric maps allow a more precise representation of areas of the same density.
- There is no risk that more dense and less dense areas cancel each other out and areas with a high density are no longer visible.
Disadvantages
- The resulting map depends on the cartographer
- The creating of dasymetric maps is time and cost consuming
- The limits of the reference areas can be uncertain.
- Dasymetric maps are not suitable for large scales because the uncertainties during the construction of the reference areas are too high.
- Direct comparison between different periods is not possible.
Choroplethic maps in relation to geometric areal units such as grid squares
Properties
Choropleth maps with regular patterns structure are
also called Choropleth maps according to
the geometric method
(Imhof 1972, p. 171)
The reference areas are built by a regular network of identical polygons like squares, triangles or hexagons. The dimensions of the polygons may vary depending on the scale and the dataset. Conceivable are hectare or square kilometre grids or even wider meshed grids. The tighter the grid, the more representative is the resulting map. If a square grid is used, it should be aligned to the national coordinate grid. Furthermore it allows an expansion to additional areas.
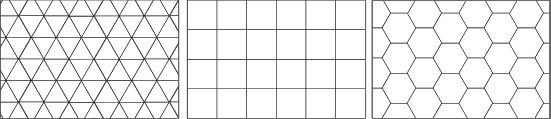 Triangle, square and hexagon grid
Triangle, square and hexagon gridThe square grid is the simplest and most widely used form of grids. The following example shows a choroplethic map using a square grid and its basic data.
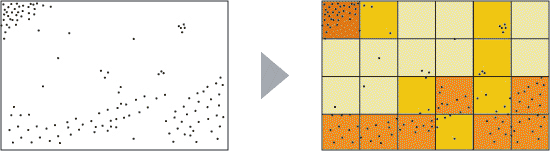
Point data with coordinates are preferably used as a basis. The Swiss Federal Statistical Office offers some raster data sets (hectare grid of the population density) which facilitates the preparation of such maps.
In the following visualisation you can see a choroplethic map based on a square grid. It depicts the percentage of shrubland per 4 km2 in Switzerland in the years 1992/1997.
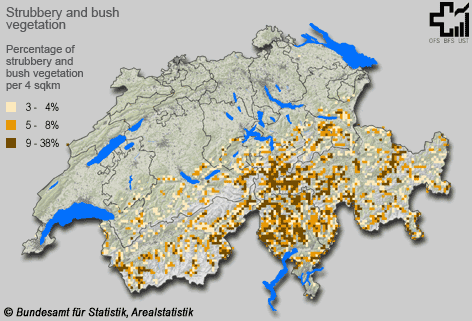
Advantages and disadvantages of choroplethic maps in relation to geometric areal units
Below the advantages and disadvantages are listed.
Advantages
- It is very simple to compare specific areas because of the constant grid.
- The comparison of different periods is possible because the reference areas do not change in time.
- An automatisation of the mapping process is possible with state of the art data processing methods (e.g. GIS) (Hake et al. 2002, p. 478).
- Because of the constant reference areas this method allows the visualisation of absolute values.
Disadvantages
- Most data are not raster data.
- The data collection process for raster data is expensive.
- The density values may vary depending on the positioning of the raster, particularly if the mesh width is large. Therefore a small mesh width is recommended.
- Natural limits (e.g. timber line) are no longer recognizable due to the raster based representation.
Generalization of choroplethic maps
For the generalisation of choroplethic maps different methods can be used individually or in combination with each other. In any case it is important to respect the minimum dimensions, which are depending on the following factors: form, colour, pattern and contour of the area. The following figure gives an overview.
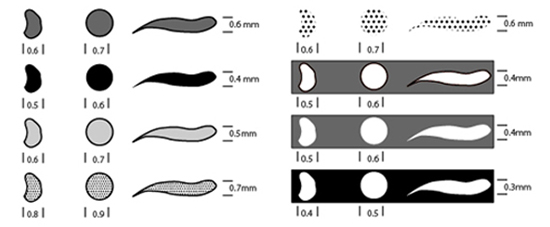 Minimal dimensions for choroplethic maps (Spiess)
Minimal dimensions for choroplethic maps (Spiess)If you get below the minimum dimensions generalisation is needed. If
administrative areas are used, it is considered to summarize the data on a
higher administrative level (summarize communities to districts, etcv). If
inhomogeneities occur, it is also possible to group certain areas. Too small
but important areas can be enlarged while maintaining an analogous shape or
aggregated with bigger neighbouring areas if the density value is only related
to settlement areas. In the second case the density value has to be recalculated.
In the case of choroplethic maps in relation to geometric areal units the mesh
width can be increased. E.g. four squares are summarized to one and the value
is recalculated. In addition the number of classes can be reduced for any
choroplethic map.
The contours of the density areas have to be simplified and smoothed according
to the scale. For choroplethic maps in relation to geometric areal units this
is not necessary because the geometries are already simplified. In general it
has to be considered that the fundamental form of the areas should not get lost
during the generalisation process and that original structures should be
preserved.
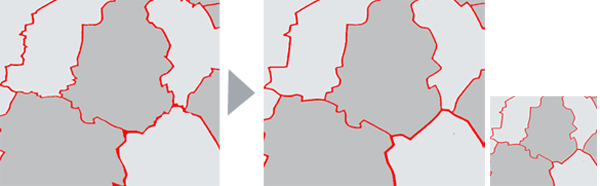 Map extract before and after the generalisation (Spiess)
Map extract before and after the generalisation (Spiess)Map examples
Now you can become more familiar with some complex examples of choroplethic maps.